数独：启智润心的数理美韵

选题背景

数学富含美学意蕴，以数学之美浸润教学是深化中小学数学课堂改革的重要途径。将数学的逻辑之美、统一之美、简洁之美、对称之美、和谐之美有机融入教学，既可以激发学生的学习兴趣，也可以启迪学生的数学思维，从而让学生更加扎实而灵动地掌握数学知识，领悟数学思想，积累数学经验，培育数学精神。

数独起源于中国先秦“洛书”的三阶幻方，蕴含阴阳五行的平衡哲学，暗合中国古代“天人合一”的宇宙观，后经阿拉伯“苏格拉底方阵”演变后，被数学家欧拉整理成9*9的网格。数独是典型的离散数学载体，其本质直观展现了数学的理性精神和人文意蕴，是开展数学美育的优质媒介。

现有研究对数独教育教学逐步深入，但仍存在局限性。一方面，许多教师未能通过历史溯源让学生在认知中华古老智慧中感受数学文化的厚重之美，美育浸润的深度和广度亟待拓展。另一方面，教学对于数独内在的逻辑之美探究还不充分。数独教学不仅要包含形式美，更核心的是通过填数规则和推理策略让学生亲身体验逻辑推导的严谨性，以及规则框架下策略选择的创造性。

教学目标

1.通过“洛书溯源—数学规则建模—策略迁移”的认知链条，让学生掌握数独基本规则（行、列、宫内数字不重复），体会数学内在的结构之美和秩序之美，领悟逻辑严谨的理性美，形成可迁移的网格推理框架。

2.通过分宫格训练，让学生建立空间秩序美，体悟理性思维的简约美，感受思维优化的迭代美。

3.通过古今数独形态对比，让学生建立符号意识和文化认同，触摸数学“古今交融”的历史传承美。

综上，本设计以“数学之美”为浸润路径，构建“历史—现实—未来”三维美育空间，在形式美、逻辑美、文化美的多维体验中，培育学生的科学精神、理性思维和文化自信，真正实现“以美育人”的教育追求。

教学设计创新

本课例以“情境化驱动、问题化探究、数学化生长”为核心创新路径，具体阐释如下。

1.情境化驱动：突破传统教学教师直接讲授的模式，以洛书神话故事为切入点，将抽象的数独规则与千年数学史联结，从学生认知根本上完成知识建构；同时以洛书溯源、数字韵律等形式美为引，既激发学生的探究兴趣，也为其注入审美基底。

2.问题化探究：遵循课堂问题链“是什么—为什么—怎样做”设计环节，通过“洛书九宫格是什么”到“为什么中宫填5”再到“古人怎么填”等具体追问，推动学生从“知其然”到“知其所以然”再到“悟其文化”的深度思考。环环相扣的问题链驱动学生“找证据”“辨差异”，进而体悟逻辑严谨美、理性简约美和人文传承美的多重意蕴。

3.数学化生长：以数学化的内在逻辑为驱动，学生在“填数—辨误—寻理”中掌握技巧，理解“有限规则创造无限可能”的辩证思想，达成“学知识”与“悟文化”双向生长，最终实现以美启智、以文化人的深层浸润。

教学实施

环节一：探秘洛书—数独的文化根脉

情境引入：播放动画《大禹与洛书》的传说，随后教师出示神龟背负的“洛书”图纹（见图1）。

图1

问1：图纹是什么？有什么含义？将图纹与数字对应填进3*3网格（见图2），给这个网格起什么样的名字会比较合理？

图2

引导学生得到数独最早的雏形—洛书九宫格（即三阶幻方）。

问2：1—9任意摆入九宫格是否可行？为什么？

引导学生感受数学的严谨性，任意摆放会破坏洛书九宫格的内在特性，即“唯一性”。

问3：固定1—9位置又衍生出什么特性？（观察行列对角线）

引导学生发现“每行、每列、对角线和都是15”的规则，感受古人智慧，初步感知洛书的九宫格与数独的内在联系。

环节二：解构“数独”—数独的解题策略

1.观数独—提取规则

教师展示四宫、六宫、九宫数独，引导学生发现特点：分别看行、列和宫，四宫1—4不重复，六宫1—6不重复，九宫1—9不重复，进而总结现代数独的规则是，不管几宫，每行、每列、每宫的数字都不能重复。

2. 填数独—寻找策略

（1）策略探索：

破解四宫初阶数独，引导学生寻找解题策略：①“唯一数法”策略；②“排除法”策略。

（2）策略对比

给出六宫数独题目，要求学生补全六宫数独第一宫，对比上述两种解题策略并谈看法，教师引导学生深度理解排除法的本质，在解题策略选择和应用中明确两种方法的适配优势—已知数少时用排除法效率高，已知数多时用唯一数法更直接。

（3）策略应用

展示六宫格数独题目（见图3），要求学生用合适的方法解题。过程中提示两点解题技巧：①行标字母列标数，如第二行第三列唤作“B3”；②数字按1、2、3……的顺序逐个排查更清晰。

图3

学生按顺序先排查1所在的行、列、宫，得到答案B6、C1、F5、D4是1。再继续排查得A4、F3、B2是2，A3、E5、F1是3，A6、B3、C2、D5、E1是4，C3、D6、E4是5。学生有序解题，巩固策略，在“唯一解”的推导中体会数学逻辑的严谨之美。

3. 数独之“独”

分小组挑战数独，其中有唯一答案数独，也有不唯一答案数独。引导学生发现3*3小数独至少需要2个不同行、不同列的已知数才能保证唯一解，帮助学生深化对数独的核心特征“独”的理解，感受数独的魅力。讲述目前数学家发现9*9的大数独至少需要17个已知数才有唯一解，提问有无更少已知数的可能，鼓励学生继续探索研究。

环节三：溯源寻根—洛书九宫格与现代数独

问：从数独追溯洛书，为何5在“中宫”（见图4）。

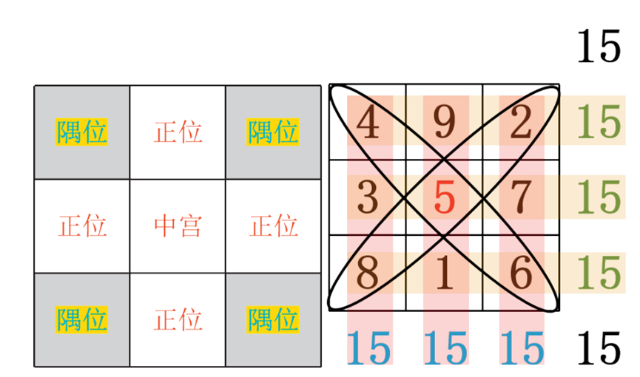
图4

教师引导学生发现5是中位数、和为15的三个数的平均数、和为15直线上的核心平衡数，进而讲解洛书以5居中构建了一种“平衡和谐”的宇宙模型，其“阴阳调和”思想，正映射数独“行列宫不重复”的平衡秩序，深化学生对中国传统数学智慧的认知，引导其感受数学文化的传承和理性之美。

环节四：礼赞“数阵文明”—数独的文化传承

1.数独的视觉美

教师向学生展示现代数独的多样化图片（见图5），引导学生欣赏数独的数理美韵和传承之美，并让学生用1—2句话分享感悟。

图5

2. 数独的生命力

问1：数独在现代有哪些作用？请你设计创作融合节气或生肖的变体数独。

教师引导学生自由创作并想象数独在现代的用途。

（张海兰系西安经开第三小学校长，周步芳系西安经开第三小学数学教师）

《人民教育》2025年第15-16期